
Some useful tips to work out the volume of solid objects
Get some useful tips to work out the volume of solid objects that means how much can be suited into an object if it is filled with a liquid or other ingredients.
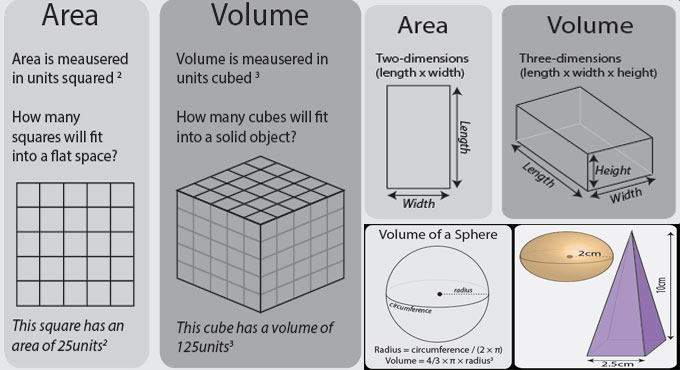
Area refers to the estimate of how much space exists inside a two dimensional object. For more information, click on Calculating Area (skillsyouneed.com/num/area.html).
Volume refers to the estimate of how much space exists inside a three-dimensional object. For more information, click on three-dimensional shapes (www.skillsyouneed.com/num/3d-shapes.html).
Practically, calculating volume can?t be applied frequently while calculating area.
By computing volume, it becomes possible to estimate, as for instance, how much packing space is required while shifting house, how much office space is required, or how much jam can be accommodated into a jar.
It is also suitable for finding out the capability of a dam or the flow of a river.
Basic formulas for working out the volume
Volume of Rectangle-Based Solids
The basic formula for determining the area of a rectangular shape is length ? width, the basic formula for volume is length ? width ? height.
The calculation remains unchanged with different types of dimensions. As for instance, apply 'depth' in place of 'height'. It should be noted that the three dimensions are multiplied together. The multiplication can be done in any order as per your choice because it won't modify the answer.
A box having the dimensions 15cm width, 25cm length and 5 cm height has a volume of:
15 ? 25 ? 5 = 1875cm3
Volume of Prisms and Cylinders
This basic formula is expanded to also include the volume of cylinders and prisms. In place of a rectangular end, you just obtain another shape: a circle for cylinders, a triangle, hexagon or, indeed, any other polygon for a prism.
In fact, for cylinders and prisms, the volume belongs to the area of one side multiplied with the depth or height of the shape.
The basic formula for volume of prisms and cylinders should be:
Area of the end shape ? the height/depth of the prism/cylinder.
Volume of Cones and Pyramids
The above method (width ? length ? height) is also applicable for working out the volume of a cone or a pyramid apart from that, as they come to a point, the volume is only a proportion of the total that it would be if they sustained in the identical shape right through.
The volume of a cone or pyramid is accurately one third of what it would be for a box or cylinder with the similar base.
The formula should be as follow:
Area of the base or end shape ? the height of the cone/pyramid ? 1/3
As for instance, to work out the volume of a cone with a radius of 5cm and a height of 10cm:
The area inside a circle = pr2 (where p (pi) is roughly 3.14 and r denotes the radius of the circle.
In this example, area of base (circle) = pr2 = 3.14 ? 5 ? 5 = 78.5cm2.
78.5 ? 10 = 785
785 ? 1/3 = 261.6667cm3
To get more information, go through the following article skillsyouneed.com

