
Procedure of Joints for Analysis of Pin-Jointed Plane Truss
In this article we are going to provide a solution about a civil engineering problem. This will be beneficial for civil engineering students and civil engineers.
The problem is as follows:
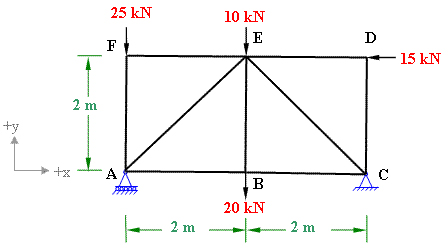
Solution:
In the above truss A is supported by roller and C is supported by hinged. First of all, we have to find out this truss?s type whether it is determinate or indeterminate.
Condition of determinacy of plane truss: m=2j ? 3
In this truss j=6 which needs 2x6-3 members for the truss to be determinate. It is clearly visible in the above figure that the truss has 9 members.
Thus the truss here is invariably determinate.
Reactions at the support:
As the support A is on the roller, so that it has no horizontal reactions except vertical reactions. On the other hand, support C is on the hinged therefore it will have both vertical and horizontal reactions.
Assuming horizontal reaction at C to be in the +ve x direction and using the conditions of static equilibrium, we obtain;
(1) ? Fx =0; so Cx ? 15 = 0 equation (1)
Solving the equation we acquire Cx = 15 kN.
(2) ? Fy = 0; yields Ay + Cy - 25 - 10 ? 20 = 0;
Ay + Cy = 55 equation (2)
(3) ? Mz = 0; considering z-axis perpendicular to the plane and passing through joint A.
Ay x 0 + Cy x 4 - CX x 0 ? 20 x 2 + 15 x 2 ? 10 x 2 + 25 x 0 = 0;
We get, Cy =7.5 kN;
Consequently Ay = 47.5 kN;
To get the complete equation solution, visit civilengineer.webinfolist.com

