How to find out the weight of steel pipes in kg
In this civil engineering tutorial, you will learn how to determine the weight of different types of pipes in Kg instantly. In this video, you will specifically learn to find out the weight of steel pipes.
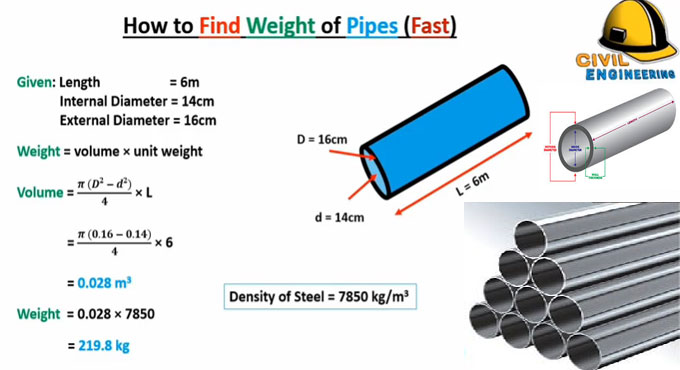
The calculation is created based on the following data :-
The length of the pipe is taken as 6 meter and represented by L.
Internal dia of the pipe is taken as 14 cm and represented by d.
External dia of the pipe is taken as 16 cm and represented by D. (External dia includes internal dia and thickness of the pipe).
The weight of the pipe will be calculated with following formula :-
Weight = Volume x Unit Weight
The formula of volume is as follow :-
Volume = p (D2 ? d2) / 4 x L
After putting the above value, we get the following :-
= p (0.16 ? 0.14) /4 x 6 (values are converted from cm to m)
= 0.028 m3
So, weight = 0.028 x 7850 = 219.8 kg.
Unit weight is also known as density and the density of steel is 7850 kg/m3.
To learn the process in detail, go through the following video tutorial.
Video Source: Civil Engineering