Estimating the Height of a Mountain
In this cutting-edge logical period, it's not hard to gauge the height of any mountain, utilization of modern GPS and satellite innovation creates enough information which can thusly accurately decide the height yet that is the supreme rise of the mountain. Nonetheless however when we talk of height we talk concerning ocean level figuring out which is in reality somewhat hard yet in the event that the ocean level is known for that geographic territory, at that point the height of a mountain can be immediately decided.
Before GPS innovation was concocted, geologists and map makers evaluated mountains with secondary school geometry and powerful protractors called theodolites and travels. On the off potential for success that you have at some known good ways from a mountain and make sense of the angle from where you are on the ground to the pinnacle, at that point you can compute its vertical height.
In the nineteenth century, British assessors in the Great Trigonometrical Survey of India estimated a specific tall mountain at 29,002 feet as they located their way over the subcontinent.
Not terrible, considering a portion of their readings were taken from 160 miles away. At the point when an American undertaking estimated Mount Everest with GPS in 1999, researchers found the mountain was 33 feet higher, or 29,035 feet above ocean level.
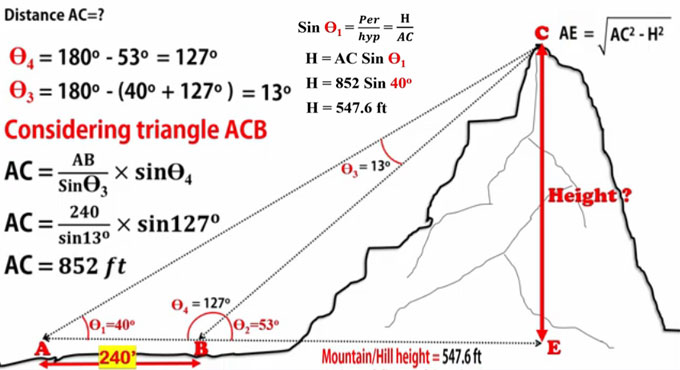
On the most fundamental level, estimating a mountain depends on essential ninth-grade math. To compute the rise of a mountain, researchers would gauge the separation between two points on the ground and afterward measure the angles between the head of the mountain and each point.
"In the event that you have two angles, you know the third, on the grounds that the whole of the angles is 180 [degrees]," Molnar revealed to Live Science.
To complete these estimations, assessors must recognize a horizontal surface utilizing a level (which, similar to the sort at a home improvement shop, depends on a caught air bubble that, affected by gravity, slides nearer to or farther away from a focal locale as it inclines). From that point, assessors eye the culmination and measure the angle with the help of a celebrated, profoundly exact protractor ? an adjustable gadget known as a theodolite. With two angles and one side of a triangle, geometry uncovers the lengths of different sides, and in this way, the height of the triangle (the mountain).
Welsh assessor and geographer Sir George Everest utilized only this monotonous method to gauge the height of the world's tallest mountain situated in the Himalayas during the 1840s. Obviously, one measure could be mixed up, so groups of geographers determined the components of the mountain from bunch various stations at the base of the mountain, averaging out the heights determined with many, numerous triangles.
Estimations depend on mathematical equations and reviewing methods that haven't changed all that much since the 1800s. On a fundamental level, estimating a mountain depends on essential ninth-grade math. To ascertain the height of a mountain, researchers measure the separation between two points on the ground and afterward measure the angles between the head of the mountain and each point.
On the off chance that you have two angles, you know the third, on the grounds that the whole of the angles is 180 degrees. To complete these estimations, assessors distinguish a horizontal surface utilizing a level.
From that point, assessors eye the culmination and measure the angle with the help of a celebrated, profoundly exact protractor ? an adaptive gadget known as a theodolite. With two angles and one side of a triangle, geometry uncovers the lengths of different sides, and along these lines, the height of the triangle (the mountain).
Obviously, one measure could get mixed up, so groups of geographers determined the components of the mountain from heap various stations at the base of the mountain, averaging out the heights determined with many, numerous triangles.
Mountain heights are estimated by various strategies beginning with looking over from a known spot's rise: you measure separations and angles. This is the reason we study trig. We additionally utilize a strategy called photogrammetry which estimates elevated photographs. A wide range of fine rakish estimation is finished by different sorts of protractors like theodolites and separations estimated by rulers, measuring tapes, laser run locaters, and radars (radio frequency matters as too long a frequency diminishes examining precision).
You don't have to have a plane or a satellite. Guide producers knew the state of Europe well before anybody flew over it, however you need to make exact estimation. In the event that you need rise, you need to concur upon a base rise (for ocean level). That is somewhat more confused than one may might suspect. You likewise need to concur upon things like the state of the Earth.
There are different studying instruments for estimation of angles and heights. Types, properties, uses and subtleties of these reviewing hardware is examined. Among the assortment of instruments that are accessible to gauge angles and heights, it is imperative to pick the best one that is more appropriate for the particular occupation. The best wellspring of data for a particular instrument is the reference of proprietor's manual or the item index that is given by the producer.
The basic gear utilized for estimating angles and rises in looking over are:
a. Hand level
b. Abney level
c. Dumpy level
d. Programmed level
e. Laser level
f. Travel method
g. Theodolite
Angle is an estimation that we can quantify between the two line which meets at a certain point. Precise estimations are assuming an essential job in estimations. The best model is that the Ships and the Airplanes will explore with the assistance of the exact precise bearings of the arrival zone. How about we talk about Angular Measuring Instruments.
Angular Measurement: As we mentioned, the angle is characterized as the opening between the two line when they correspond at a certain point. The essential unit for the Angular estimation is Degree (?). In the event that a circle is isolated into 360 equivalent parts by a line passing through the inside. at that point each part can be called as a Degree (?).
1. Every degree (?) partitioned into an hour (').
2. Every moment (') partitioned into 60 seconds (").
3. Another unit for the angle is Radian.
4. Radian characterized as the angle at the focal point of a circular segment whose length is equivalent to the span of the arc (Circle).
For Angular estimations, there are a wide assortment of gadgets accessible in metrology. Be that as it may, the estimating gadget can be favored dependent on the sort of the segment to be estimated, and the precision and precession required in the estimations. The precision of the gadget is minimal check of every gadget. Protractors are the populated instruments utilized for the rakish estimations.
A straightforward Protractor is a fundamental gadget for rakish estimations. Best case scenario, A straightforward protractor can give minimal tally of one degree (1?) for littler protractor and a large portion of a degree (0.5?) for huge protractors.
There is a wide assortment of protractors accessible, out of them vernier slant protractor is most populated one. A customary Vernier angle protractor can peruse up to 2.5 minutes (0.04?) where as an optical protractor can peruse as long as 2 minutes (0.03?).
Following are the diverse Angular Measuring Instruments:
a. Vernier Bevel Protractor
b. Optical Bevel Protractor
c. General Bevel Protractor
d. Sine Bar
e. Angle Gauges
f. Clinometer
g. Angle Dekker
h. Auto Collimator
To get more details, go through the following video tutorial.