How to design reinforced concrete diaphragms for wind

This is a useful technical brief for all the civil engineers that briefly explains the concept of reinforced concrete diaphragms.

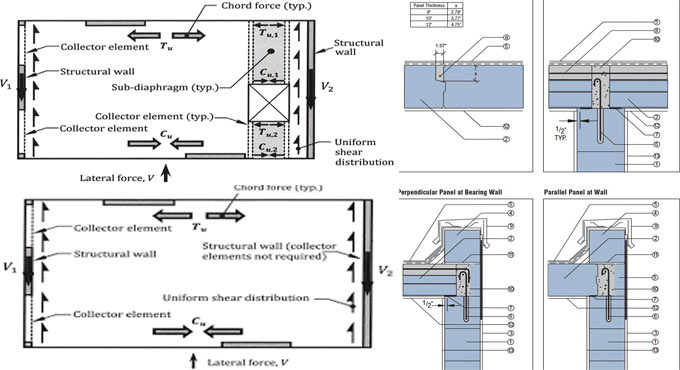
To cope up with seismic loading, floor and roof systems in reinforced concrete (RC) buildings function as diaphragms to deliver the lateral earthquake loads to the vertical lateral force-resisting system (LFRS). In recent times, horizontal diaphragms are generally accepted to be rigid. Consequently, the impact of their in-plane movement concerning the vertical LFRS is ignored.

A precast concrete diaphragm comprises of precast components having unnecessary cast-in-place pour strips along some or all boundaries and with or without cast-in-place topping slabs.

Reinforced concrete diaphragms (related to floors and roofs) regarding a structure attach the vertical structural components (like walls and frames) collectively so that the buildings can withstand outside loads like gravity and lateral forces from seismic events or wind action.

Floor diaphragms are very crucial for transmitting the forces from the structure to the lateral force defiant components which then move the forces from the structure to the ground. The magnitudes of internal forces inside concrete floor diaphragms are significantly more complicated as compared to those supposed by some basic methods which are applied in current design practice, like the Equivalent Static Analysis (ESA) method. The ESA method is mostly found in structural design.

Cast-in-place, reinforced concrete slabs having standard ratios and span lengths can generally be taken as rigid diaphragms. It signifies that the lateral forces are transmitted to the components of the LFRS corresponding to their proportional rigidities. In systems where beams or ribs exist ? like in wide-module, two-way joist and grillage systems ? the components underneath the slab allow to harden the diaphragm even further.

With adherence to the American Concrete Institute?s ACI 318, Section 12.3, diaphragms should contain enough thickness to fulfill all related strength and serviceability requirements. Normally, the thickness of a floor or roof system is initially set on the basis of the strength and serviceability requirements with respect to gravity loads. That thickness is normally enough to fulfill equivalent requirements for the combined factored load effects (gravity plus lateral) on the diaphragm.

Diaphragm Forces - There exist two primary forces in diaphragms, which are known as inertial forces from the accelerations of the floors and transfer forces which originate from incompatible deformation patterns from various lateral force countering systems inside the structure. The type of lateral force resisting systems and the geometry of the structure will state which of these forces, inertia or transfer, will lead.

To get more details, go through the following exclusive construction article www.structuremag.org