How to work out the area of different types of triangles
This civil engineering tutorial provides some vital guidelines for calculating the areas of different types of triangles.
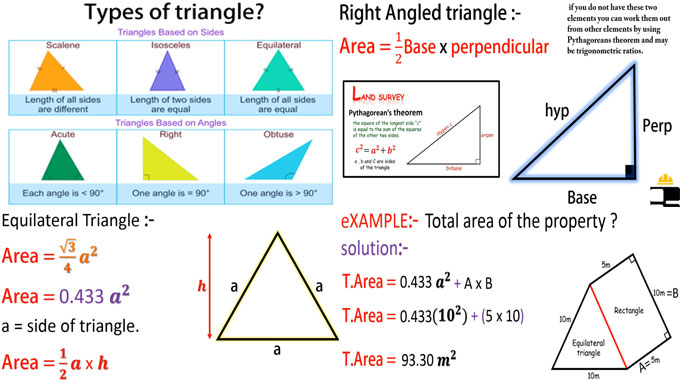
Classification of triangles - On the basis of sides:
1. Scalene ? Length of all sides are not same.
2. Isosceles ? Length of two sides are equivalent.
3. Equilateral ? Length of all sides are equivalent.
On the basis of angles:
1. Acute - Each angle remains less than 90 degree.
2. Right ? One angle is equal to 90 degree.
3. Obtuse ? One angle is greater than 90 degree.
The areas of different types of triangles are calculated as follow :-
Right Angle Triangle :- Area = ? Base x Perpendicular
So, base and perpendicular must exist for right angle triangle. If these components are not available, the calculation of area can be done from other elements by applying Pythagoreans theorem as well as trigonometric ratios.
Pythagorean theorem - The square of the lengthier side ?c? is equivalent to the sum of the squares of the other two sides.
c2 = a2 + b2
Equilateral Triangle :-
Area = v3 / 4a2
Area = 0.433 a2 (a denotes the side of the triangle)
This formula is applicable when the value of the side of equilateral triangle is given. But when the value is unknown and but perpendicular is given, then the calculation of area should be done with the following formula :-
Area = ? a x h
Besides, the area can also be calculated with triagonometric ratios or triagonometric identities.
Isosceles Triangle - If the sides of the triangle are given, the measure the perpendicular with Pythagoras theorem and find out the area with the following formula:
a2 = h2 + (b/2)2
h2 = a2 - (b/2)2
Area = ? Base x perpendicular
Area = ? b x h
Scalene Triangle : The area of this type of triangle is calculated with Hero formula as follow -
Area = vs(s-a)(s-b)(s-c) [here S denotes the semi parameter of the triangle and abc are the sides of triangle)
S = a+b+c / 2
To get more details, go through the following video tutorial.
Video Source: SL Khan/a>