How to work out the cutting length of the triangular stirrups
Bar Bending Schedule, also known as ?BBS? comprises of an extensive list that briefly specifies the location, mark, type, size, length and number, and bending details of each bar or fabric in a Reinforcement Drawing of a Structure.
This method of itemizing the location, type and size, number of and all other details is termed as ?Scheduling?. With regard to Reinforcement bars, it is known as bar scheduling. In a nutshell, Bar Bending Schedule is a system of arranging rebars for each structural unit, providing detailed reinforcement requirements.
Cutting Length Of The Triangular Stirrups:
Given below, some vital guidelines for working out the cutting length of triangular stirrup :-
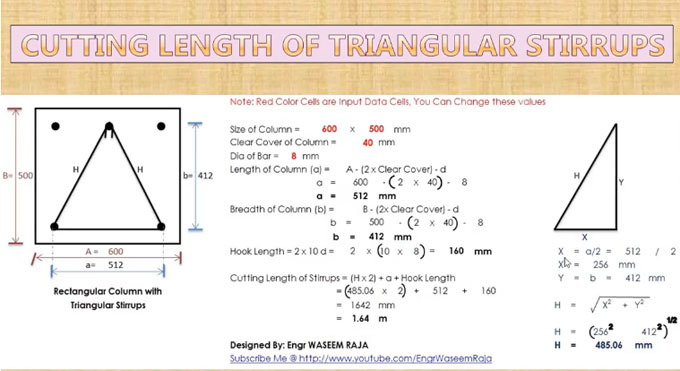
Suppose, the length of the column is 600 mm and width 500 mm. Diameter (represented as d) of the stirrup is taken as 8 mm.
Clear cover for both sides is provided as 40 mm. Center to center length of the main bars is given as a (512 mm) and center to center width is given as b (412 mm).
The detail method is provide below to know how the above center to center values are originated :-
a = 600 ? (2 x 40) ? (2 x 4) (4 signifies half of diameter 8 mm) = 512 mm
b = 500 ? (2 x 40) ? (2 x 4) (4 signifies half of diameter 8 mm) = 412 mm
The cutting length is determined with the formula given below :-
= (2 x H) + a + (2x10xd) (since there exist two hooks and length of one hook is 10 mm; dia denotes dia of stirrups) ? (4x3xd) (since there exist 4 bends and each bend is situated at 90 degree angle and for each bend 3d is subtracted)
By applying the Pythagorean theorem, the value of H is determined. It refers to a basic relation in Euclidean geometry among the three sides of a right triangle.
It states that the square of the hypotenuse (the side is situated opposite of the right angle) is equivalent to the sum of the squares of the other two sides.
To get more details, go through the following video tutorial.
Video Source: Engr WASEEM RAJA